[반도체공정 feat.jaeger] 확산(Diffusion) Chapter 4.2.1~4.2.3 - 원료의 확산(constant source diffusion)

반도체 8대 공정 순서

1. 실리콘 웨이퍼 제조 공정
2. 산화공정(Oxidation)
3. 포토공정(Photo)
4. 식각공정(Etching)
5. 증착공정(Deposition)
     - 확산(Deposition)
     - 이온주입(Ion implantation) 
6. 금속배선공정(Metalliztion)
7. EDS 공정(Electrical Die Sorting)
8. 패키지공정(Package)

---

 

기판도 불순물을 받아들이는 정도가 있습니다.

우리는 이것을 solid solubility(고용도)라고 부릅니다.

 

책에서는 고용도를 N₀라고 정의합니다.

 

기판에 도핑을 하려고 할 때 2가지 상황을 고려할 수 있습니다.

 

1. 불순물이 계속 투입이 될 때.

2. 불순물의 투입이 도중 중단될 때.

 

즉 확산법도 달라지게 됩니다.

반도체 공정은 아주 세밀화되어 있어 변수요소 하나하나가 아주 중요합니다.

4.2.1. 일정원료 확산 (constant source diffusion)

---

일정원료 이상 과다하게 불순물을 계속해서 공급할 때 고용도가 제한됩니다.

figure 4.2

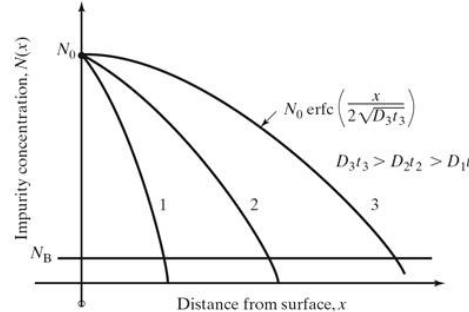
y축 : 불순물 농도.

x축 : 기판으로 부터 떨어진 거리.

 

t=0일 때 불순물은 아직 주입조차 안되었습니다. 따라서

N(x,0) = 0

t>0일 때 불순물 주입이 시작되므로,

N(0, t) = N₀

 

위의 경계조건을 바탕으로 Fick의 제2법칙을 풀면 다음과 같은 식이 도출됩니다.

일정 원료 확산 식

erfc : complementary error function

D : diifusion coefficient(확산계수)

 

왼쪽 figure 4.4, 오른쪽 figure 4.6

 

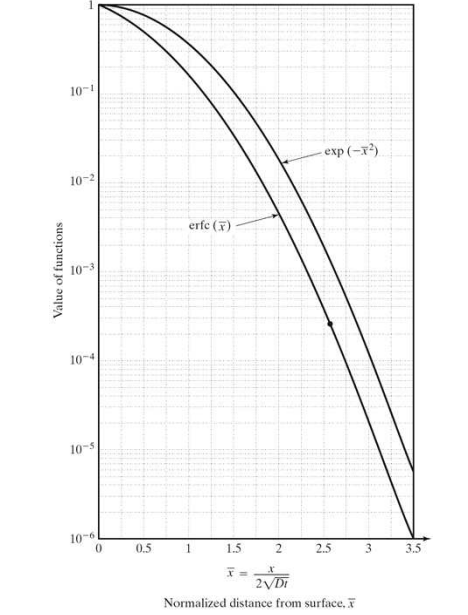
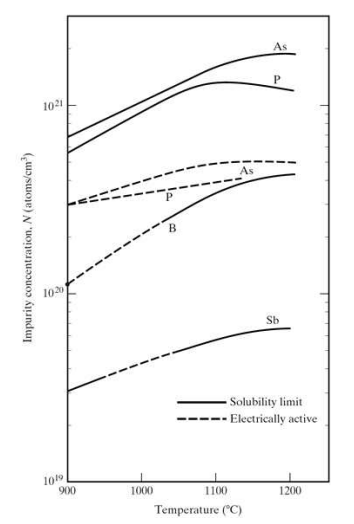
왼쪽은 erfc(complementary error function)의 함수를 그래프로 나타낸 것입니다.

오른쪽은 온도에 따른 여러가지 도핑 불순물이 가진 고용도 그래프입니다.

 

여기서 잠깐, erfc 함수 그래프 x축에서 하나 주의할 게 있습니다.

 

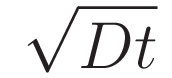
: diffusion length(평균확산거리)

 

 

평균확산거리는 반도체를 설계할 때 중요한 변수입니다.

 

4.2.2. 제한 원료 확산 (limited source diffusion)

---

불순물 원료의 공급이 중단될 때, 즉 기판에 불순물이 어느정도 남아 있으나 더 이상의 추가적인 공급이 차단될 때 확산시키는 방법입니다.

이 확산법의 불순물 분포도는 Gauss분포를 띄게 됩니다.

 

반도체 공정에서는 공정상 편리성 때문에 선확산 후 후확산을 진행합니다.

 

첫 번째 확산인 선확산(pre diffusion) 때는 짧은 시간 일정 원료 확산을 하고,

두 번째 확산인 후확산(drive-in diffusion) 때는 긴 시간동안 제한 원료 확산을,

 

이렇게 이단 공정을 진행합니다.

 

그렇다면 이제 선확산 부터 진행하겠습니다.

 

먼저 선확산 때 투입될 총 불순물의 양을 Q라고 정의합니다.

Q는 다음과 같이 쓸 수 있습니다.

 

 

 

 

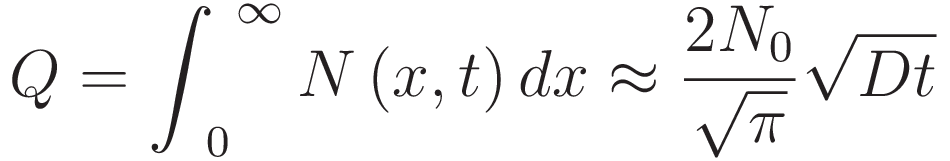
이렇게 단위 면적당 총 불순물 양 Q를 Dose라고 부릅니다.

여기서 선확산과 후확산을 나눠 Fick 제2법칙을 이용하면 다음과 같은 식이 도출됩니다.

t₁ D₁ (선확산시간, 선확산계수)

t₂, D₂ (후확산시간, 후확산계수)

 

 

 

 

 

figure 4.3

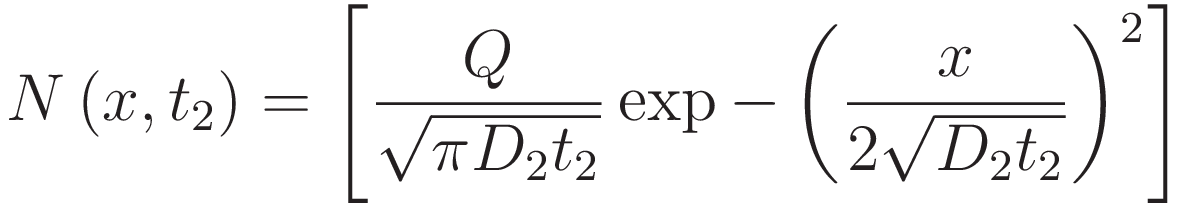
여기에 위의 Q 식을 대입하면 다음과 같은 식으로 정리됩니다.

 

제한 원료 확산 식

 

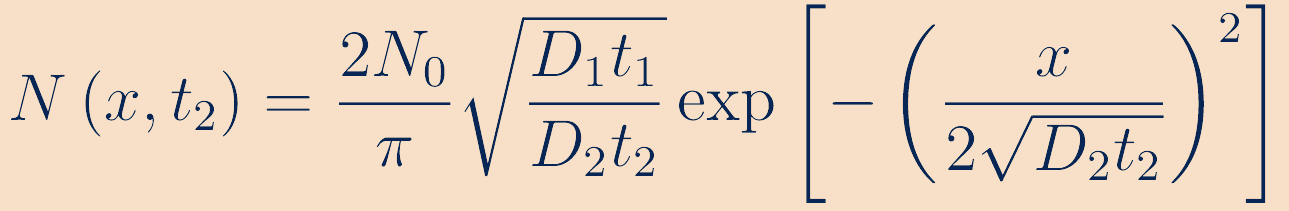
다시 살펴보면, 위 식은 확산 후 불순물 도핑농도 함수입니다.

식 가운데의 루트부분은 선확산과 후확산의 평균 거리 비율을 나타내는 것을 확인할 수 있습니다.

 

만약 분모가 분자보다 작다면 N(x, t)은 우상향 함수가 됩니다.

기판으로부터 멀어질 수록 도핑 농도가 늘어난다? 말도 안 됩니다.

+필자의 주관으로는 아마 선확산 때 짧은 시간인 이유가 이 내용과 관련 있지 않을까 생각합니다..

 

즉 

 

 

 

의 조건에서 유효한 식입니다.

 

즉 이 식은 평균 선확산 거리보다 평균 후확산 거리가 훨씬 클 때 유효하다는 결론입니다.

 

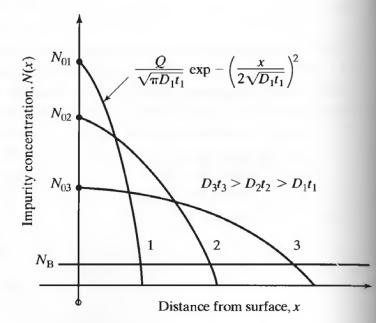
그림 4.3을 보면 선확산이 농도는 높으나 깊이는 짧습니다.

후확산은 농도가 낮으나 깊이가 깁니다.

 

따라서 같은 양의 도핑을 했을 때 분포는 다르나 면적은 같습니다.

 

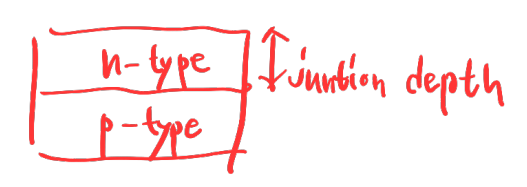
4.2.3. 접합깊이 (junction depth)

---

figure 4.3

 

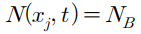
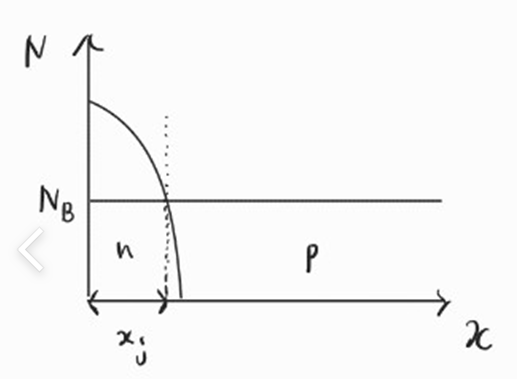
일 때 xⱼ 를 junction depth라고 합니다.

 

여기서 N_B는 반도체 기판의 불순물 농도입니다.

예를 들어 불순물농도가 10^17cm^-3인 p 형 기판에서 n 형 불순물을 확산하였을 때를 생각해 보겠습니다.

 

위의 그림에서 xⱼ 보다 작은 지역은 n형이고 xⱼ 보다 큰 지역은 p형 지역이 되어 p/n 접합 구조가 완성됩니다.

 

아래 그림을 보면 이해가 좀 더 쉬울 것 같습니다.

 

junction depth는 또 역시 2가지로 구분해 계산해야 합니다.

 

1. 선확산 접합 깊이(junction depth)

 

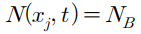
에서, 그리고

 

일정원료 확산 식에 xⱼ 를 대입해 다시 보겠습니다.

 

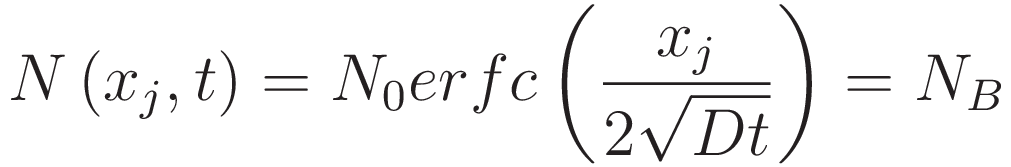
에서 xⱼ에 대한 식으로 다시 정리하면 다음과 같습니다.

 

선확산 junction depth

 

 

 

 

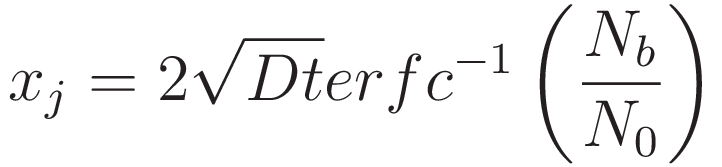
2. 후확산 접합 깊이(junction depth)

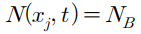
에서, 그리고

 

제한 원료 확산 식에 xⱼ 를 대입해 다시 보겠습니다.

 

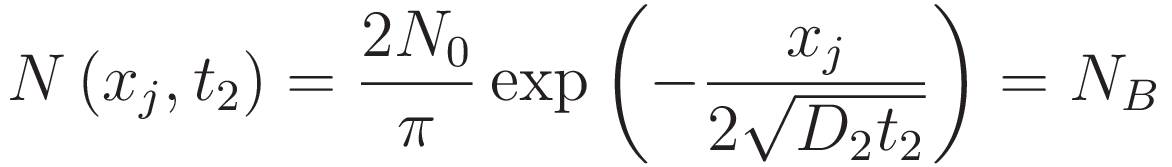
에서 xⱼ에 대한 식으로 다시 정리하면 다음과 같습니다.

 

 

후확산 junction depth

 

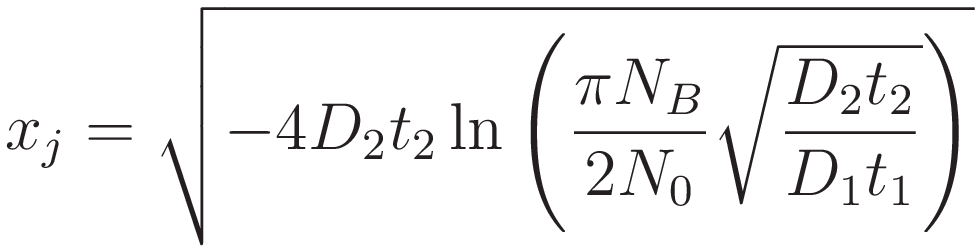
4.2 예제

---

 

 

 

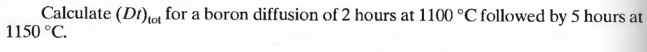
보론(B)을 2시간 동안 1100℃ 선확산과 5시간 동안 1150 ℃ 후확산 후의 평균확산거리 총합을 구하시오.

풀이 참고용

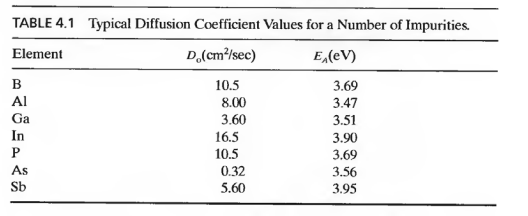
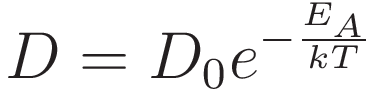
solution:

---

긴 글 읽어주셔서 감사합니다.

 

 

introduction to microelectronic fabrication (Vol 5)

For courses in Theory and Fabrication of Integrated Circuits.The author's goal in writing this text was to present a concise survey of the most up-to-date techniques in the field. It is devoted exclusively to processing, and is highlighted by careful explanations, clear, simple language, and numerous fully-solved example problems. This work assumes a minimal knowledge of integrated circuits and of terminal behavior of electronic components such as resistors, diodes, and MOS and bipolar transistors.

저자

jaeger

출판

피어슨 에듀케이션

출판일

2013.08.30