동전 배팅 필승법

 

확률 배팅.

 

특히

 

"동전 던지기"

 

이기면 2배 지면 잃는 간단한 게임.

이 게임에는 허점이 존재하고 있다.

---

 

50%의 승률을 가진 "coin tossing"은

과연 필승법이 존재할까?

 

이 '필승법'은

약 99.99%의 승률을 보인다.

 

 

---

 

 

흰색은 앞 면

 

 

 

대표사진 삭제

 

 

검은색은 뒷 면

 

 

 

 

필요한 것은 3단계 규칙.

 

1. 원하는 가격을 배팅.

 

 

저는 뒷 면에 200원을 건다.

확률은 이러할 것.

 

 

아쉽게도 흰 면-200

 

여기서 제곱하여 400원을 뒷 면에 배팅.

 

여기서 갈린다.

 

진다면 총 -600 손해

 

그러나 이긴다면 총 +200 이득 왜?

 

1회차에서 200을 걸고 패배

2회차에서 400을 배팅했고

지면 -600 이기면 +800 이기 때문.

 

표로 보자.

 

2회 차 진행할 동안 벌어지는 경우 2P2이다.

표로 보면 이러하다.

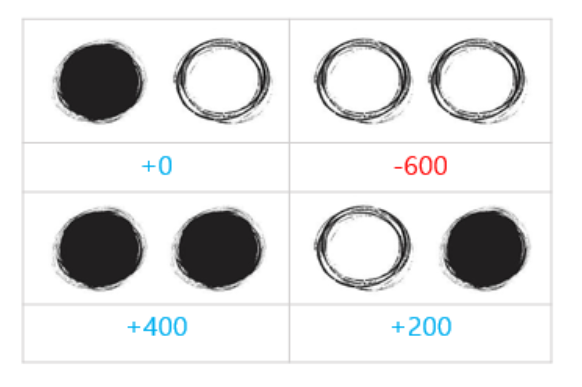
져도 상관없다. 무한으로 근사해야 성립하는 필승법인 것이다.

+0원도 사실상 이득이라고 보면 된다. 그렇다면 겉으로만 볼 때 패배 확률은 25%.

 

 

2. 패배(n) 할 때마다 아래의 식 대로 배팅.

 

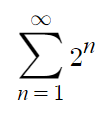
예를 들어 일단 3 연속패배를 가정할 대. 패배 시 원금(나의 경우 200원)의 2n배씩 배팅한다.

1회 -200

2회 -400

3회 -800

 

총 -1400 손해.

 

만약

 

 

4회 차에서 원금의 24배인 1600을 걸고 승리한다면.

4회 +3200

 

이미 배팅하여 없어진 1600원까지 합해서 총 투자한 지출금액은 -3000

하지만 4회 차 승리로 인해 +3200이다. 결과적으로 총 +200 이득인 것이다

 

 

마지막으로

 

3. 게임에서 승리하면 규칙 1부터 반복

 

결과적으로 볼 때 항상 +200 이득이다.

---

 

이 방법에 장점과 단점이 보일 것이다.

 

큰 배팅을 하기엔 위험 부담이 너무 크다.

2n으로 배팅하기 때문에 적은 돈으로 하는 게 안정적으로 보인다.

 

그래서 끈기가 필요하다.

그래도 티끌 모아 태산 아닌가?

 

충분하다.

 

 

만들어본 c++코딩 소스,

아래의 프로그램으로 분석해 보았는데 원금의 약 1/10로 시작하는 것이 가장 안정적이고 효율적이었다.

 

#include  <stdio.h>
#include  <stdlib.h>
#include  <time.h>
int main() {
    srand(time(NULL));
    int tmp, random;
    int c=0, hap1= 0, hap2= 0, i, f;
    printf("배팅할 금액 :");
    scanf_s("%d", &f);
    for (i = 0; i < 10; i++) {
        random = rand() % 2;
        if (random == 1)
        {
            hap1 += f;
            printf("%d회차 맞았음 +%d\n", i, f);
         
                f = 200;
            continue;
        }
            
            printf("%d회차 틀렸음 -%d\n", i, f);
            hap2 += f;
            f = f * 2;
    }
    printf("총 이익 : +%d\n", hap1);
    printf("총 손해 : -%d\n", hap2);
    printf("총 손익 : %d\n", hap1-hap2);


    /*도와주신 분 : 유령137*/
}

 

10번 동전을 던졌을 때 경우이다 만약 마지막에 무조건 이긴다면 절대 손해란 존재하지 않는다.

 

 

이 배팅을 "마틴 배팅"이라고 한다.

 

그러나 이 배팅의 문제점은 자본이 엄청나게 필요할뿐더러 운이 안 좋으면 모든 재산을 탕진하는데 까지 매우 빠른 시간이 걸린다는 점이다.

 

 

+이전 블로그에서 가져와 재 업로드했습니다.