기술은 감각이다, 밀론 블로그
몬티홀 문제의 증명 [파이썬] 본문
몬티홀 문제가 뭘까요?
간단하게 확률 문제입니다. 사람을 단번에 호구로 만들어 버릴 수 있지만 말입니다.
'인간은 합리적이다!'라는 관점으로 보는 주류 경제학의 뒤통수를 때려버린 재밌는 문제입니다.
'반드시 합리적이지는 않다!'라는 관점으로 보는 행동 경제학에게 힘을 실어주는 문제이기도 합니다.
본론으로 들어와서 몬티홀 문제에 대해 이야기 해봅시다.
당신이 고를 수 있는 문이 3개있다.
1개의 문에는 람보르기니.
그 중 2개의 문에는 염소.
사회자가 당신보고 문을 1개 선택하라한다.
문을 열고 나온 물체는 당신 소유라고 한다.
당신이 문 1개를 선택했다고 치자. 그 때 사회자가 염소가 있는 아무 문 1개를 열어버렸다.
여기서 사회자가 말하기를 "기회 줄테니. 선택한 문 바꿔도 됨. 할래 말래?"
자 진짜로 선택의 순간이 왔다.
선택한 문을 고수할 것인가. 변경할 것인가.
따지고 보면 결국엔 두 문만 남은것 아닌가?
겉으로 보는 이 문제의 확률 결과는 각각 50%로 보인다.
그래서 50%아니냐고? 한번 실험해보자. 파이썬으로 증명이 가능하다.
import random
n = int(input("please write here number of games to be played : "))
m = [1,2,3]
i=0
a=0
b=0
a1=0
b1=0
for i in range(n):
i=i+1
random.shuffle(m) #a[0]= 1, a[1]=0, a[2]=0 *1 for winning, 0 for bang.*
x = int(random.uniform(1,4)) # your choice
# when not change selection.
if x == m[0]:
a=a+1
#print("you win")
elif x == m[1]:
b=b+1
#print("you lose")
else:
#print("you lose")
b=b+1
# when change selection.
if x == m[0]:
a1=a1+1
#print("you lose")
elif x == m[1]:
b1=b1+1
#print("you win")
else:
#print("you win")
b1=b1+1
#when not change selection.
hap=int((a/(a+b))*100)
print("in "+str(n)+" games when not change")
print("selection was you win percentage : "+str(hap)+"% \n")
#when change selection.
hap1=int((b1/(a1+b1))*100)
print("in "+str(n)+" games when change")
print("selection was you win percentage : "+str(hap1)+"%")
#done
n번의 게임 동안
'고수', '변경'의 선택 평균 승률을 구하는 코딩이다.
게임을 1번 만 돌려보자.
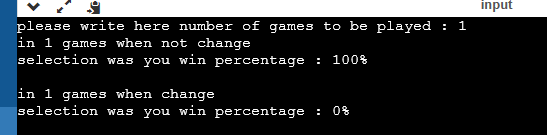
안타깝게도 '고수'의 선택이 이겼다. 그러나 이걸론 신뢰할 수 없다.
좀 더 반복 시행하여 평균을 가져보자.
10번 만 돌려보자.
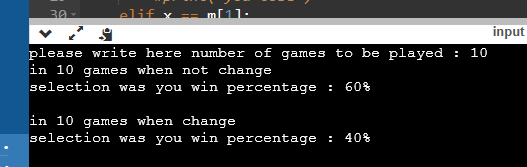
'고수'의 승률이 더 높다. 정말인가? 더 돌려보자.
100회 게임을 진행한다.
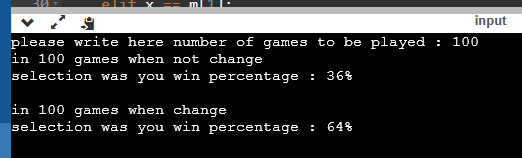
이번엔 '변경'의 선택이 이겼다.
1000회 가보자.
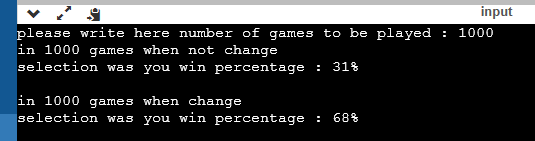
아까와 변화가 거의 없다. 10000회 가보자.
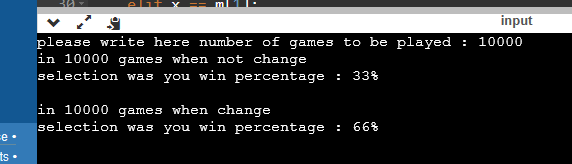
정확히 1:2 비율이 나왔다. 게임 횟수를 더 높여도 변함이 없는 비율 이었다.
필자는 이 문제를 처음 봤을 때 '고수'의 선택이 더 나은 결과라고 판단했었는데 보기 좋게 틀렸다.
그래서 이 결과가 말하고자 하는게 뭘까?
왜 선택을 바꾼놈이 고수한놈 보다 2배 승률이 높냐는 말이다.
조건부 확률로 보면 경우의 수가 다음 표와 같이 정리할 수 있다.
| 당첨 | 당첨 | |
| 꽝 | 당첨 | |
| 꽝 | 당첨 |
0은 사회자가 꽝을 열어버린 문이다.
T이 색은 당신이 고른 문이다.
자 선택을 고수해보자. 파란글자 확률은? 1/3이다.
자 선택을 바꿔보자. 검은 글자를 선택한 것이다. 2/3이다.
만약 문의 수가 많아진다면 어떤 일이 벌어질까?
1만개의 문과 당첨 1개. 9,999개의 꽝 문을 열어버린다. 선택을 고수할 것인가? 변경할 것인가?
'수학 > 증명' 카테고리의 다른 글
| 동전 배팅 필승법 (0) | 2024.07.10 |
|---|---|
| 국제 수학 올림피아드 난제 PART - 1 [ IMO 2011 P2] (0) | 2023.08.21 |


