국제 수학 올림피아드 난제 PART - 1 [ IMO 2011 P2]

보통 올림피아드는 보통 대수, 조합, 기하, 정수 기준으로 문제를 출제하는데 비해 이번 IMO 2011 P2는 해석학적 추론을 요구하는 통찰력 문제이다.

 

그렇게 대단한 수학적 지식을 필요하지는 않다. 즉 일반적인 사람들도 건드려볼만한 문제라는 것이다.

그러나 쉽게 볼 수는 없다.

 

왜 난제이겠는가?

국제 수학 올림피아드(IMO) 2011년 2번 문제.

문제를 보자.

Problem 2

Let $$[math(\cal S)]$$be a finite set of at least two points in the plane. Assume that no three points of $$[math(\cal S)]$$ are collinear. A windmill is a process that starts with a line ℓ going through a single point $$[math(P\in\cal S)]$$. The line rotates clockwise about the pivot P until the first time that the line meets some other point belonging to $$[math(\cal S)]$$. This point, Q, takes over as the new pivot, and the line now rotates clockwise about Q, until it next meets a point of $$[math(\cal S)]$$. This process continues indefinitely.
Show that we can choose a point P in $$[math(\cal S)]$$ and a line ℓ going through P such that the resulting windmill uses each point of $$[math(\cal S)]$$ as a pivot infinitely many times.

영문

 

 

문제 2

평면 위의 두 개 이상의 유한 개의 점으로 이루어진 집합 $$[math(\cal S)]$$가 있다. 이 집합의 어느 세 점도 일직선 위에 있지 않다. 풍차란 다음과 같은 과정을 의미한다: $$[math(\cal S)]$$ 중의 단 한 점 P를 지나는 직선 ℓ로부터 시작하여, P를 회전의 중심으로 하여 ℓ을 시계방향으로 회전시키다가 이 직선이 처음으로 $$[math(\cal S)]$$에 속하는 다른 점 Q를 만나면, 다시 Q를 새로운 회전중심으로 하여 시계방향으로 회전을 계속 진행한다. 이러한 진행을 $$[math(\cal S)]$$의 점들을 회전중심으로 하여 무한 번 계속한다.
적당한 $$[math(P\in\cal S)]$$와 이 점을 지나는 적당한 직선에서 시작된 풍차가 $$[math(\cal S)]$$의 각 점들을 회전중심으로 무한히 여러 번 사용하게 됨을 보여라.

국문

 

이..무슨?

 

한국 선수들은 잘했을까?

 

IMO 2011 대한민국 성적

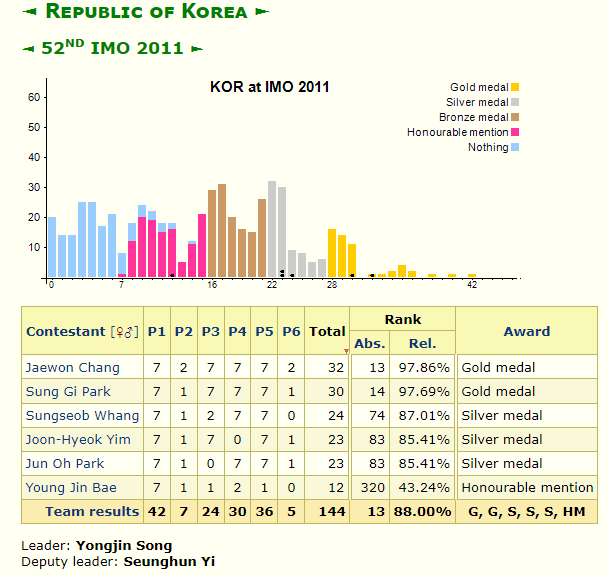
문제 2번(P2)만 유난히 점수가 처참하다.

 

채점 기준은 7점 만점이고 P2는 평균 1점으로 채점이 되었다.

 

IMO는 4시간 30분씩 이틀에 걸쳐 시험을 보며 하루에 3문제씩 출제되고 시험시간은 오전 9시에서 오후 1시 30분까지 4시간 30분이다. 다시 말해 도합 9시간 동안 총 6문제를 푸는 것이다

 

최소 90분 동안 P2를 풀어야 한다.

---

 

문제 2

평면 위의 두 개 이상의 유한 개의 점으로 이루어진 집합 $$[math(\cal S)]$$가 있다. 이 집합의 어느 세 점도 일직선 위에 있지 않다. 풍차란 다음과 같은 과정을 의미한다: $$[math(\cal S)]$$ 중의 단 한 점 P를 지나는 직선 ℓ로부터 시작하여, P를 회전의 중심으로 하여 ℓ을 시계방향으로 회전시키다가 이 직선이 처음으로 $$[math(\cal S)]$$에 속하는 다른 점 Q를 만나면, 다시 Q를 새로운 회전중심으로 하여 시계방향으로 회전을 계속 진행한다. 이러한 진행을 $$[math(\cal S)]$$의 점들을 회전중심으로 하여 무한 번 계속한다.
적당한 $$[math(P\in\cal S)]$$와 이 점을 지나는 적당한 직선에서 시작된 풍차가 $$[math(\cal S)]$$의 각 점들을 회전중심으로 무한히 여러 번 사용하게 됨을 보여라.

국문

 

문제를 간단히 설명하자면

 

이제 무한히 긴 직선 ℓ을 임의의 점인 P에 올려둘 것이다.

이 직선은 풍차처럼 시계방향으로 회전한다.

 

점에 닿은 직선은 그 점을 중심으로 회전 중심을 변경한다.

이 현상이 반복된다.

 

이 직선은 모든 점을 닿고 무한히 여러번 회전함을 증명하라.

 

 

이 문제를 해설 없이 혼자 풀어보라.

몰입하게 되고 스스로의 통찰력을 테스트하게 된다.

 

이 문제를 하루 내에 풀었다면 통찰력이 꽤나 좋은 편이다. 자랑해도 좋다.

 

 

이 문제는 다음 포스팅에서 다루겠다.