수학 교육과정을 대폭 줄일 수학 기호 triangle of power.

 

지수.$$ A^2 $$

 

로그.$$ \log _a{b} $$​​

 

제곱근.​$$ \sqrt[b]{a} $$

 

 

중학교 교육과정에서 학습하게 되는 수학 기호들이다.

필자 또한 똑같은 과정을 경험했다.

 

우리는 이 세가지 기호를 이해하고 익숙해지기 위해 많은 시간을 투자했다.

 

 

 

하나의 규칙을 설명하기위해 세가지 기호를 사용함으로써

세번의 공부를 하게 만들었고

세번의 고통을 겪게 만들었다.

 

만약 하나의 기호로 이를

 

설명 할 수 있다면?

배우기도 쉽다면?

 

그렇다면

 

우린 아마 가까운 길을 멀리 돌아간 것일지도 모르겠다.

 

 

독자 당신의 생각 아래 이 기호가 쓸모있다 판단된다면, 또한 특별해지고 싶다면.

 

이 글을 보아라.

 

---

이 세가지 기호들은 서로 상호작용하며 본질적으론 같은 역할을 한다.

 

$$ x^y=z $$​

수의 제곱을 계산하기 위해 지수를사용하고

 

$$ \sqrt[y]{z}=x $$

지수의 역수를 구하기 위해 제곱근을 사용하고

 

$$ \log _x{z}=y $$​

지수 값을 구하기 위해 로그를 사용한다.

 

서로가 연관한다.

 

이놈들은 우리를 곤란하게 만들었다.

 

이 글에서 보여줄 단 하나의 기호만 숙지 하여도 위 세가지 기호들은 굳이 배울 필요가 없음을 깨닫게 해주고자 설명한다.

 

그 기호는 바로 triangle of power이다.

 

필자의 편의를 위해 긴 이름을 줄여서 class.

즉 클래스라고 부르겠다

 

모양은 이렇다.

 

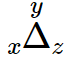
이 삼각형 하나로 세가지 원리를 동시 설명할 수 있다.

 

예를 들어

$$ 2^3=8$$​

을 보자. 이것은

 

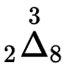
으로 나타낼 수 있다.

 

2는 상수를 뜻하고,

3은 지수를 뜻하며,

8은 2의 3승 값을 뜻한다.

 

사진 삭제

사진 설명을 입력하세요.

이렇게 표현도 가능하다.

 

간단한 예제,

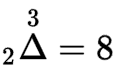
8의 3제곱근 이므로, 2가 되겠다.

 

 

마지막으로 3가지 기호와 클래스 기호를 비교하면,

 

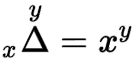
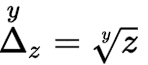
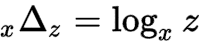
로 표현 가능하다.

 

정말 아름답다! 더욱 놀라운 것은 시각적 예술이다.

 

이걸 한번 봐보자.

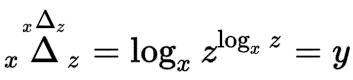
이런 식으로 나아갈 수 있다.

 

어떠한가?

학창시절 우리를 애먹인 저 3가지 놈들을 보아라. 이제 로그를 볼 필요가 없다.

 

아래는 이 기호에 호기심을 품은 사람에게 더 자세한 설명을 주는 좋은 사이트이다.

 

The Triangle of Power

아래 영상은 이 블로그를 쓰게 만든 장본인이다.

 

 

우리는 좀 더 생각해보아야 한다.

과연 이 기호가 기존의 기호보다 실용적이고 시각적으로 더 나은가?

 

경로의존성에 의해 보류되는 것일 수 있다.

필자는 고민해볼만하다고 생각한다.