기술은 감각이다, 밀론 블로그
집합의 모순 - 러셀의 역설 본문
집합론 다들 배웠을 것이다.

위 그림은 집합 A, B의 교집합을 표시한 것이다.
집합은 독일의 수학자 칸토어가 처음 사용하였고 영국의 수학자 버트런드 러셀에 의해 기호가 사용되었다.
이 집합론에는 아주 '치명적인 오류'가 있었다.
이 오류를 지적한 사람이 바로 아까 언급한 영국의 수학자 버트런드 러셀.

그 오류는 집합이 가지는 역설이었다. 모순이 있었던 것이다.
러셀은 1901년 5월이나 6월에 칸토어의 논문을 검토하는 과정에서 이 역설을 발견하였다.
역설은 아래와 같다.
'자기 자신을 원소로 포함할 수 없는 집합'들의 집합 A라고 R을 정의.
이 정의는 다음과 같이 표시 될 수 있다.

집합 A안에는 무수히 많은 원소가 있다. 다음과 같이 표시할 수 있다.
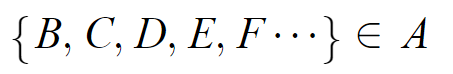
이 원소들은 전부 자기 자신을 포함하지 않는 집합들이다.
여기서 B를 꺼내보자.

B안에는 B가 포함될 수 없다. C역시 같을 것이고 B, C, D, E, F · · · 들도 같을 것이다.
그렇다면 여기서 A안에 A가 포함될 수 있을까? 그게 가능할까?
한번 확인 해보자.

A를 A안에 원소로 포함 시켰다. 그런데, 맨 처음 정의했던 R.

분명 A안에는 A가 포함될 수 없다고 했다. 모순이 된다. · · · 증명 ①
그렇다면 빼자.
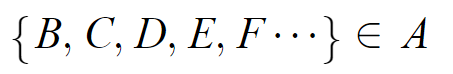
이렇게 되면 이제 집합 A는 자기 자신을 포함시키지 않는다. 그런데 이상하다.
맨 처음 했던 정의를 다시 보자.
'자기 자신을 원소로 포함할 수 없는 집합'들의 집합 A라고 R을 정의.
여기서 말하는 A는 '자기 자신을 원소로 포함할 수 없는 집합'이지 않은가?
A는 자기 자신을 포함하지 않는 집합이 되어 버렸다. 그렇다면 집합 A에 포함될 수 있다는 말이된다.

다시 들어왔다.
근데 이렇게 되면 아까 했던 증명 ①에 의해 모순이 된다.
즉 A는 자기 자신을 제외할 수도 포함할 수도 없어진다는 말이다. 그 자체로 모순이 발생한다.
이것이 바로 러셀의 역설이다.
이 역설을 들은 학자들의 반응은 말그대로 혼돈 그 자체였다고한다. 공리가 무너졌다라고 말이다.
이후 집합의 정의를 수정하여 역설을 방지했다고 한다.

어떤가요? 이해가 되시나요?
독자가 학생이시라면 학교에서 토론해보세요.
뉴턴이 있으라! Q.E.D.
'수학' 카테고리의 다른 글
| 수학 교육과정을 대폭 줄일 수학 기호 triangle of power. (0) | 2023.08.28 |
|---|---|
| 당신의 통찰력은? [대장장이의 쇠고리] (0) | 2023.08.05 |


