기술은 감각이다, 밀론 블로그
양자역학 1장 확률[Griffiths] 본문
양자역학에서 가장 기본적으로 알아야할 지식이 있습니다.
확률입니다.
파동함수에 대해 언급하고 확률을 이용한 파동함수 이해 과정을 통해 공식을 유도할 것입니다.
이어 예제를 통해 개념을 단단히 하겠습니다.
입자가 존재하는 확률. 즉 어떠한 공간에서 입자가 존재할 가능성.
바로 '파동방정식(Ψ)'이다.
양자역학이 무엇인가?
말그대로 미시계에서 이루어지는 양자의 운동을 설명하고 이해하고자 하는 학문이다. 이와 맞 교전을 벌이는 고전역학은 거시계에서 다루어지는 운동 역학이다. 양자역학에서 입자는 항상 관측되기 전엔 파동 상태로 존재하고 관측되는 순간 입자로 변한다고 주장한다.
파동방정식은 일에너지 방정식과 비슷하다. 질량 (m)인 물체가 있고 위치 (x)와 받는 함력 (F)가 주어지면 시간 (t)에 대한 f(x)를 모두 구할 수 있다. 파동 방정식 또한 조건이 주어지면 입자가 존재할 위치를 확률적으로 알 수 있다는 것이다.
입자의 존재 확률 분포는 다음의 파동함수 제곱으로 나타낼 수 있다. 이유는 나중에 설명하겠다.
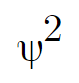
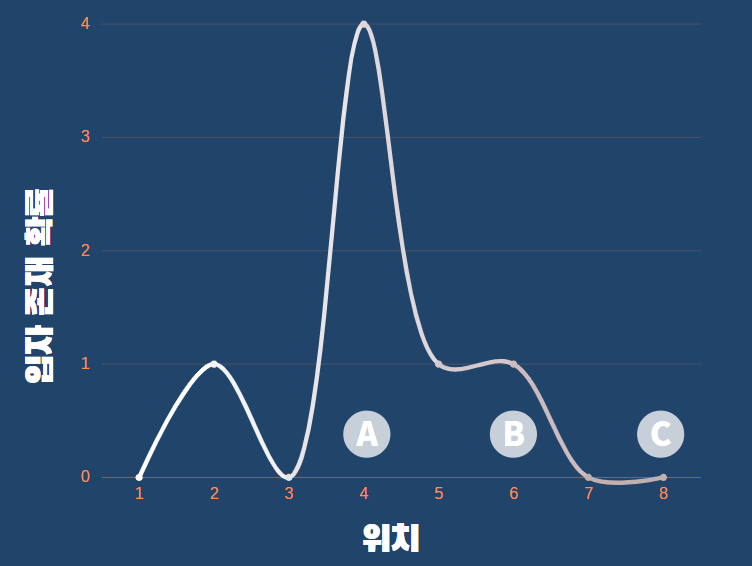
위 이미지를 보라. 위치 (x)에 따른 입자 존재 확률 분포(ψ^2)의 그래프이다.
입자는 위치 B, C에서 보다 위치 A에서 관측될 가능성이 높다.
여기서 질문이 있다. 만약 입자가 위치 B에서 관측되었다면, 관측 이전에는 어디에서 존재했는가?
이 질문에서 학자들은 3가지 대답을 보인다.
사실주의적 관점
"위치 B에 존재했다."
대표적인 학자로는 아인슈타인이 있다. 위치 B에 있었는데 양자역학은 그 사실을 알려주지 않으므로 불완전한 이론이라는 말이다.
정통주의적 관점
"입자의 위치는 모른다."
입자는 파동 상태로 확률적으로 분포하는데 관측을 하는 순간 입자가 생성이 된다라는 느낌이다.
불가지론적 관점
"묵비권을 행사하겠다."
의외로 이 태도는 어리석지않다. 애초에 '관측 전 상태'를 어떻게 아는가? 모순아니냐? 그냥 의미없는 행위이다. 라는 것이다.
양자역학을 믿는 학자들에게 질문을 날리면 정통주의적 관점의 태도를 보이다가 언젠가 불가지론적 관점의 태도를 보인다.
이 파동방정식을 이해하기 위해선 양자역학에서 사용되는 확률을 먼저 이해할 필요성이있다.
즉 확률 개념을 짚고 넘어가야한다.
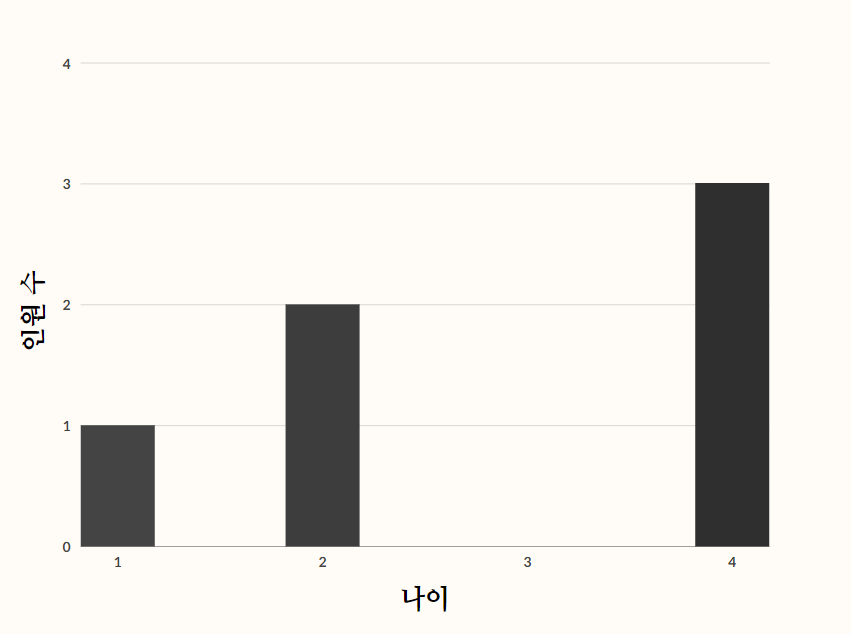
여기 나이에 따른 인원 수 표가 있다.
임의의 나이를 j. ( j= 1살, 2살, 4살 )
j에 따른 인원수를 N(j). ( N(1) = 1명, N(2) = 2명, N(4) = 3명 )
인원 수 전체 합을 N. ( N(1) + N(2) + N(4) = 6명 )
이라고 정의할 때,
여기서 임의로 아무나 뽑았을 때 2살일 확률은? 1/3이다.
즉 임의로 아무나 뽑았을 때 나이 j일 확률P(j)은?
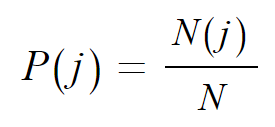
그렇다면, 나이의 평균은 얼마인가?
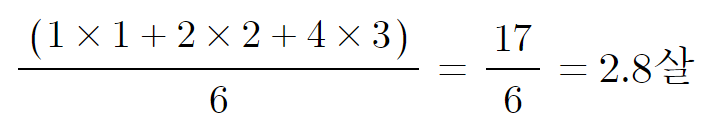
이를 공식화 시켜보면 다음과 같이 나타낼 수 있다.
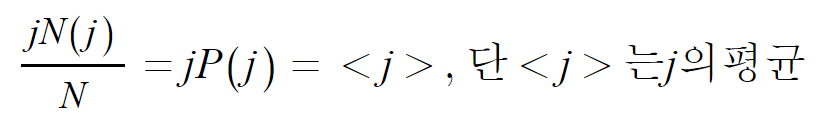
반면 중간값은 얼마인가? 3명보다 나이가 적고 3명보다 나이가 큰 3살이 중간값이다.
중간값과 평균값은 엄연히 다르다. 주의하라.
여기서 P(j)를 전부 더하면 다음과 같다.
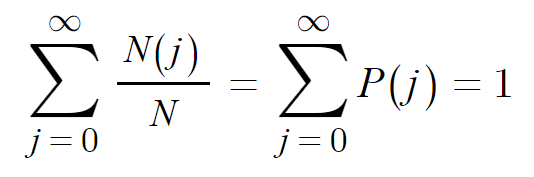
당연히 모든 확률의 합은 1이다.
평균은 문제가 있다. 다음 표를 보라.
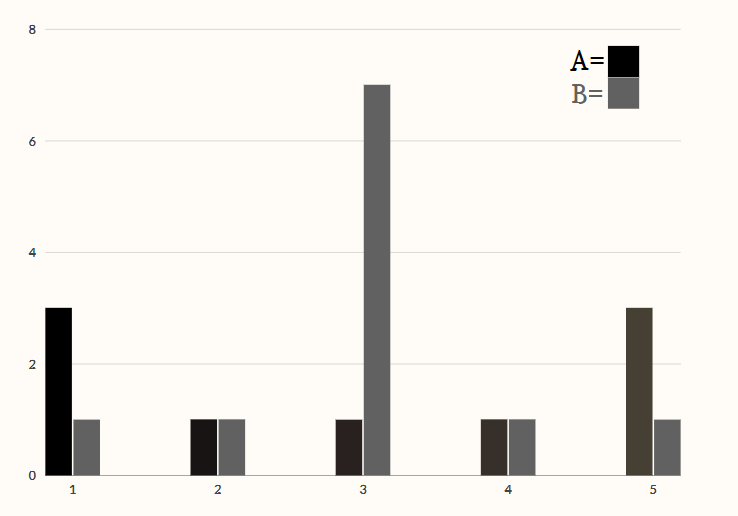
차트 A와 B의 평균은 같다.
두 표의 차이를 나타내기 위해서는
편차를 구하면 된다.
σ = j - <j>
로 나타낼 수 있다.
편차의 평균을 구해보자.
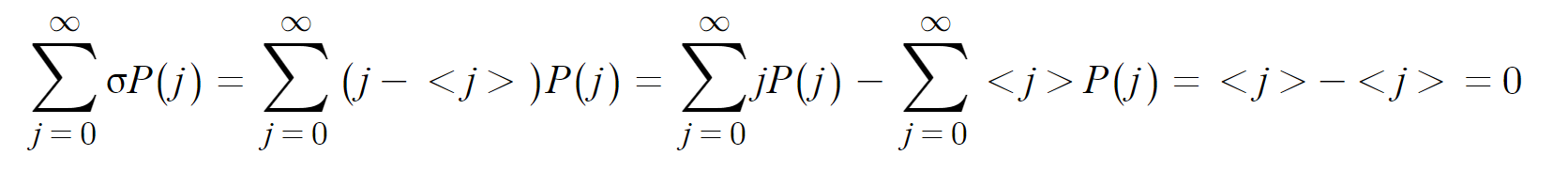
이렇게 편차의 평균은 0이 나오게 된다. 골때리는 상황이다.
다른 방법도 있지만 그건 조금 더 골때리게 되니 편차에 제곱(σ2)을 시켜 해결 해주는 것이 편하다.
간과해서는 안될 것이있다. 평균의 제곱과 제곱의 평균은 다르다. 예를 들어
1살, 3살의 평균의 제곱은 4이다. 제곱의 평균은 5이다. 다르다.
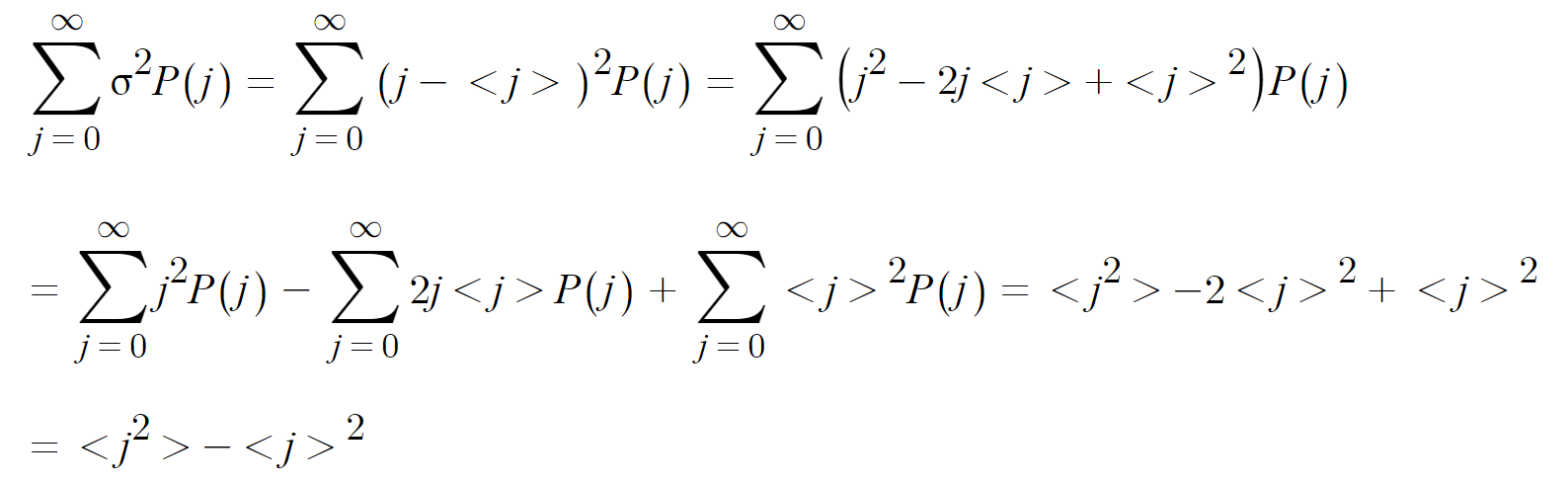
로 정리가 가능하다. 제곱근을 해주면 표준편차가 나온다.
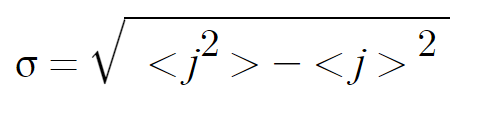
간결하게 잘 나왔다.
우리는 보통의 경우 제곱의 평균이 평균의 제곱보다 크다는 것을 아까 살펴보았다.
σ = 0이라면 퍼지지 않았다는 말이다. 입자 존재 확률 그래프가 가운데로 솟은 모양의 그래프를 보일 것이다.
즉 입자가 발견된 곳이라고 봐도 될듯하다. 반대로 시그마가 클 수록 입자 발견확률이 낮아진다라고 봐도 될듯 싶다.
여기까지가 불연속의 경우이다. (위 에서 나이는 j라는 정수이므로)
이제 연속적인 경우를 살펴보자. 불연속일 때 보다 좀 더 보편적이다.
*책에선 사람을 임의로 선택해 특정 나이일 경우로 설명한다.
지구에서 아무나 1명 골라 나이가 정확히 16년 1일 33초일 경우는 0에 수렴한다.
하지만 16살과 16살 2일 에서 찾을 경우 확률은 올라간다. 간격을 좁힌 것이다.
여기서 아무나 1명 골랐는데 16살~16살 2일 일 확률은 16살~16살 1일에서 찾을 확률의 2배일 것이다. 간격에 비례하고 확률에 비레한다.
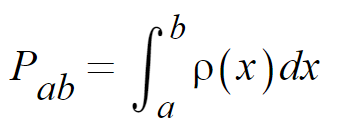
따라서 {x와 x+dx사이에서 개인이 있을 확률}을 {ρ(x)dx의 적분}으로 나타낼 수 있다.
a에서 b사이 간격이 커질 수록 뽑을 확률은 비례한다.
p(x)라는 확률밀도가 커질 수록 뽑을 확률은 비례한다.
왜 적분인가? 그래프로 볼 수 있기 때문이다.
예를들어 ρ(x)=x.
0 에서 1 사이일때 Pab=1/2이다.
x = 0에서는 확률 0.
x = 1에서는 확률 1.
a-b간격에서의 확률이니 적분값 즉 여기서의 평균값 1/2인 것이다.
이를 불연속적 분포에서 구한 규칙들을 적용 시키면 다음과 같은 상태로 바꿀수 있다.
연속적 분포의 확률 공식.
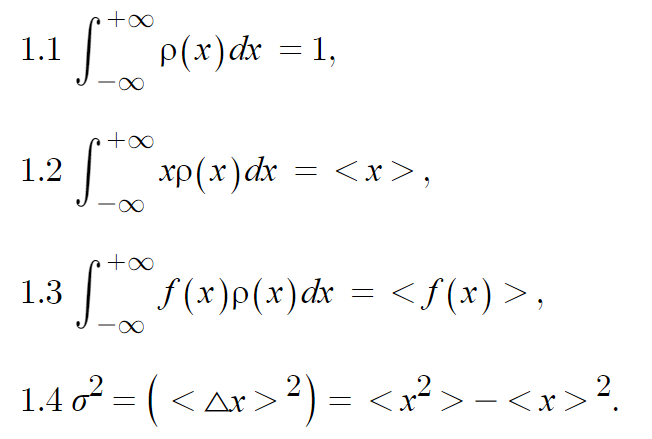
책의 예제 1.2로 조금만 더 숙련해보자.
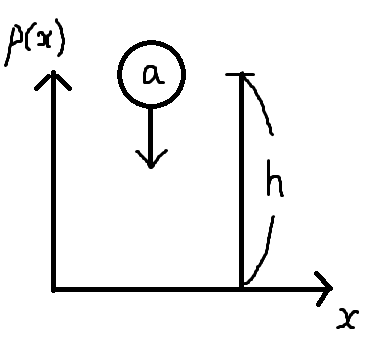
물체 a라는 바위를 높이 h인 절벽에서
떨어뜨린다.
떨어지는 동안 임의의 시간간격 동안 백만장의 사진을 찍는다.
각 사진에서 바위가 떨어진 거리를 측정한다.
문제. 이 모든 거리의 평균은 얼마인가? 즉 지나간 시간 평균은 얼마인가?
바닥에 도착하기 까지의 전체시간 T 동안 언제인지는 모르지만 확률적으로 임의의 Δt동안은 사진 백만장을 찍어댈 것이다. = Δt/T
또한 이에 해당하는 범위. 즉 총 이동하는 거리 h동안 사진 프레임 간의 거리가 있을 것이다.
그리고 책에서는 평균거리가 h/2보다는 작을 것이라 예상한다. 이유는 좀 전에 봤던
예로 p(x)=x, 0 에서 1 사이일때 Pab=1/2이다.
0에서는 확률 0, 1에서는 확률 1이다. a-b간격에서의 확률이니 평균값인 1/2인 것이다.
를 보면 이해가 쉽다. 정지한 물체가 떨어진다. 즉 속력이 점점 증가한다.
속력 0에서 v까지 즉 평균 속도는 1/2라는 것이다. s=vt이므로 평균거리 또한 반토막이 난다. 따라서 극단적으로 사진 1백만장을 T동안 찍어대도 평균거리는 h/2를 넘기지 못한다는 것이다. 당연하다.
T 동안 t와 t+Δt사이에 찍힐 확률. = Δt/T
= 이에 해당하는 범위 x와 x+Δx사이에 있을 확률. = ρ(x)dx
Δt/T에 대한 x의 식. 이 놈만 구해주면 끝이다.
풀어낼 놈을 정했으니 이제 정리해서 구해보자.
시간 t에서 거리 x 는 다음과 같다.
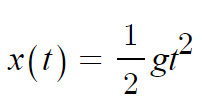
속도는 Δx/Δt = gt. 즉
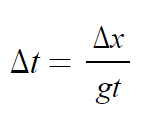
이다. 이제 대입할 일만 남았다.
전체시간 T과 대칭되는 x(t),
사진 찍을 간격 t와 t+Δt사이와 대칭 되는 Δx/gt.
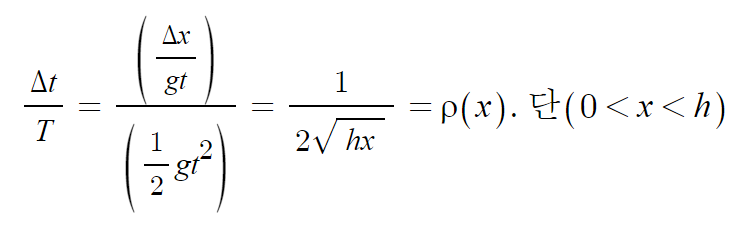
위의 연속적확률공식 1.1을 이용해보면,
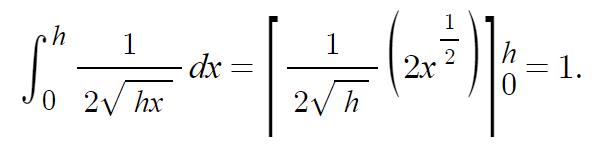
를 확인할 수 있다.
이제 평균거리를 연속적확률공식 1.2를 이용해서 구해보자.
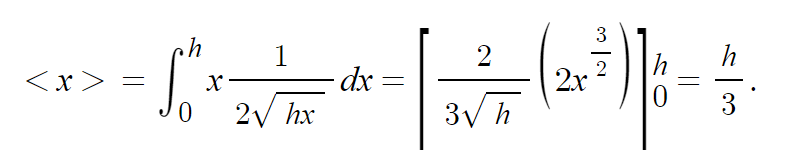
아까 책에서 에상한대로 2/h를 넘지않는다. 좋았다.
확률밀도 ρ(x)를 그래프로 나타내보자. h=1이라 가정한다.
그래프를 그려보면 다음과 같이 나타난다.
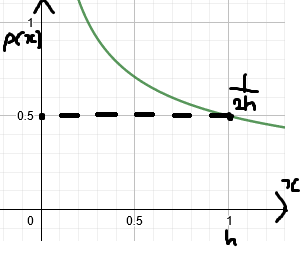
공식 1.1은 유한한데 (1보단 작고 0보단 큰) 확률밀도 ρ(x)는 무한할 수 있다고 한다.
이 다음 배울 것은 규격화라는 것에 대해 다룰 것이다.

책 : Introduction to Quantum Mechanics 3판, David J. Griffiths.
뉴턴이 있으라! Q.E.D.
'양자역학' 카테고리의 다른 글
| 양자역학 [슈뢰딩거의 고양이] (1) | 2023.07.09 |
|---|

